Self-organized network of phase oscillators coupled by activity-dependent interactions

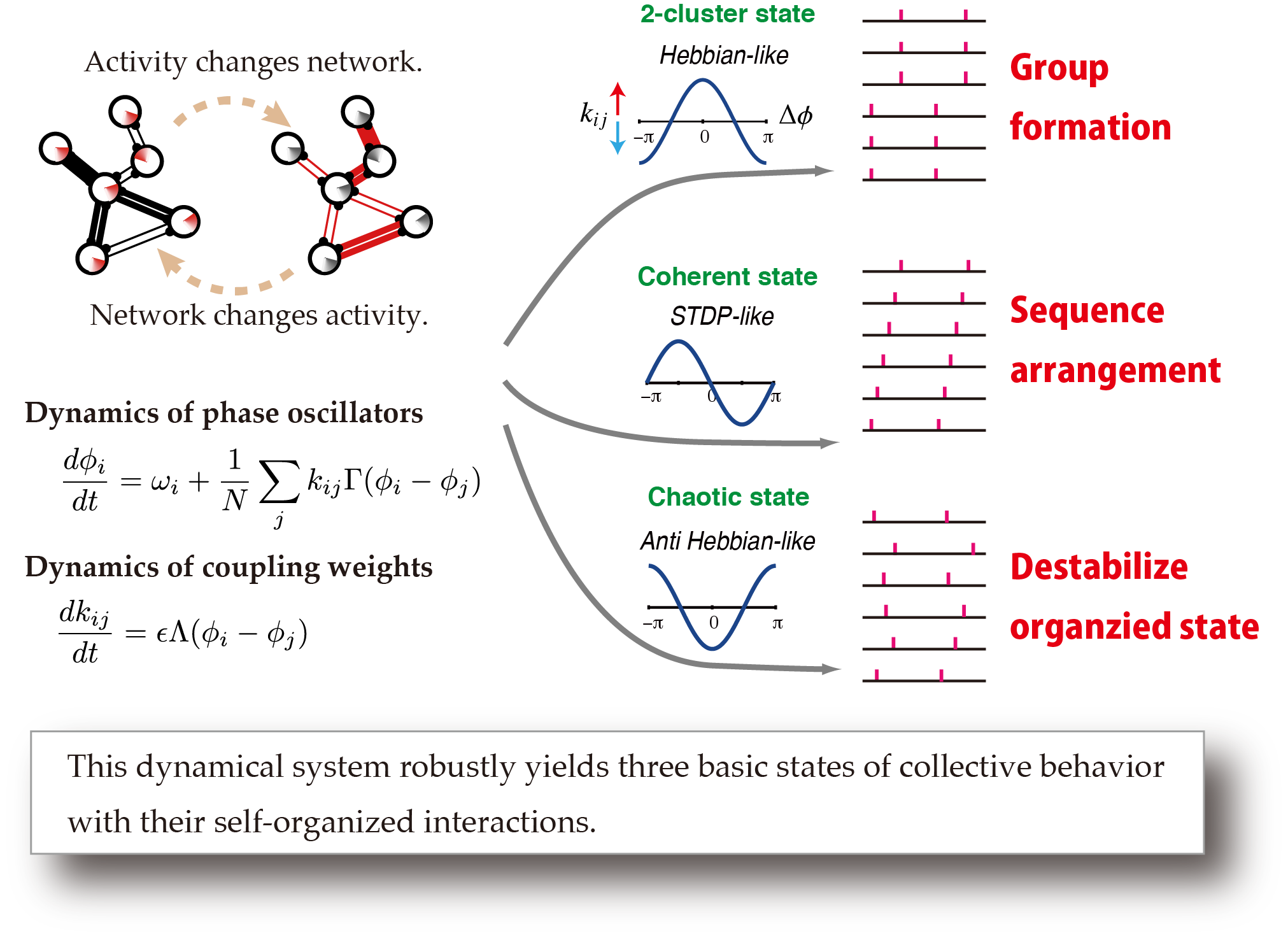
The adaptivity of neural network is based on synaptic plasticity, through which the neuronal activity induces changes in the network connections. On the other hand, the underlying synaptic network significantly affects the neuronal activity. The purpose of this research is to understand this interplay between neurons and synapses. We constructed a theoretical model of oscillatory neurons coupled with activity-dependent synaptic connections and analyzed the effects of synaptic plasticity on the network organization.

We investigated a network of coupled phase oscillators whose interactions evolve dynamically depending on the relative phases between the oscillators. We found that this co-evolving dynamical system robustly yields three basic states of collective behavior with their self-organized interactions. The first is the two-cluster state, in which the oscillators are organized into two synchronized groups. The second is the coherent state, in which the oscillators are arranged sequentially in time. The third is the chaotic state, in which the relative phases between oscillators and their coupling weights are chaotically shuffled. Furthermore, we demonstrate that self-assembled multiclusters can be designed by controlling the weight dynamics. We expect that these results will provide new insight into self-assembly mechanisms by which the collective behavior of a rhythmic system emerges as a result of the dynamics of adaptive interactions.

Literature

• Co-evolution of phases and connection strengths in a network of phase oscillators, Takaaki AOKI and Toshio AOYAGI,
  Physical Review Letters, vol.102, 034101 (2009).
  DOI: 10.1103/PhysRevLett.102.034101

• Self-organized network of phase oscillators coupled by activity-dependent interactions, Takaaki AOKI , Koichiro YAWATA and Toshio AOYAGI,
  Physical Review E, vol. 84, Issue 6, 066109 (2011).
  DOI: 10.1103/PhysRevE.84.066109

tags: AdaptiveNetworks, Co-Evolving-Dynamics, PhaseOscillator, KuramotoModel, Synchronization, Spike-Timing-DependentPlasticity, (STDP)